如有疑问请先阅读本文档,仍有疑问请加用户QQ群862194587
注册即送1元免费额度(为防止批量获取试用额度,请使用QQ邮箱注册)
可直接使用所有模型,点击聊天即可马上体验
模型计费全部公开透明,日志中每一条详情都可显示具体的计费过程
如需调用API服务,将 https://api.bailili.top/ 和默认key填入应用接口即可使用,无需代理
为保证数据库快速读取,日志可能将于每月2号清理,如对日志有异议请提前联系
数据看板统计结果和令牌的已用额度仅供参考,与日志有出入的以日志为准
日志下载(按令牌)https://query.bailili.top/
本站为促进人工智能的发展和落地应用,供开发者使用,仅可个人使用或用于学术研究,严禁用于对外服务等其他用途
请自觉遵守《生成式人工智能服务管理暂行办法》,严禁使用api进行非法行为,一经发现,立即封号
模型定价说明
由于注册已赠送1元测试额度,请先确认能否连通使用,能否满足自己需求后再充值,本站没有义务提供技术支持,非本站原因恕不退款。
注册后的默认令牌auto分组:auto分组的令牌即可访问全站所有模型,并按模型所在分组计费,除特殊需求,无需创建其他分组的令牌。
充值1元兑换本平台1$,分组倍率为1即代表1元1刀。
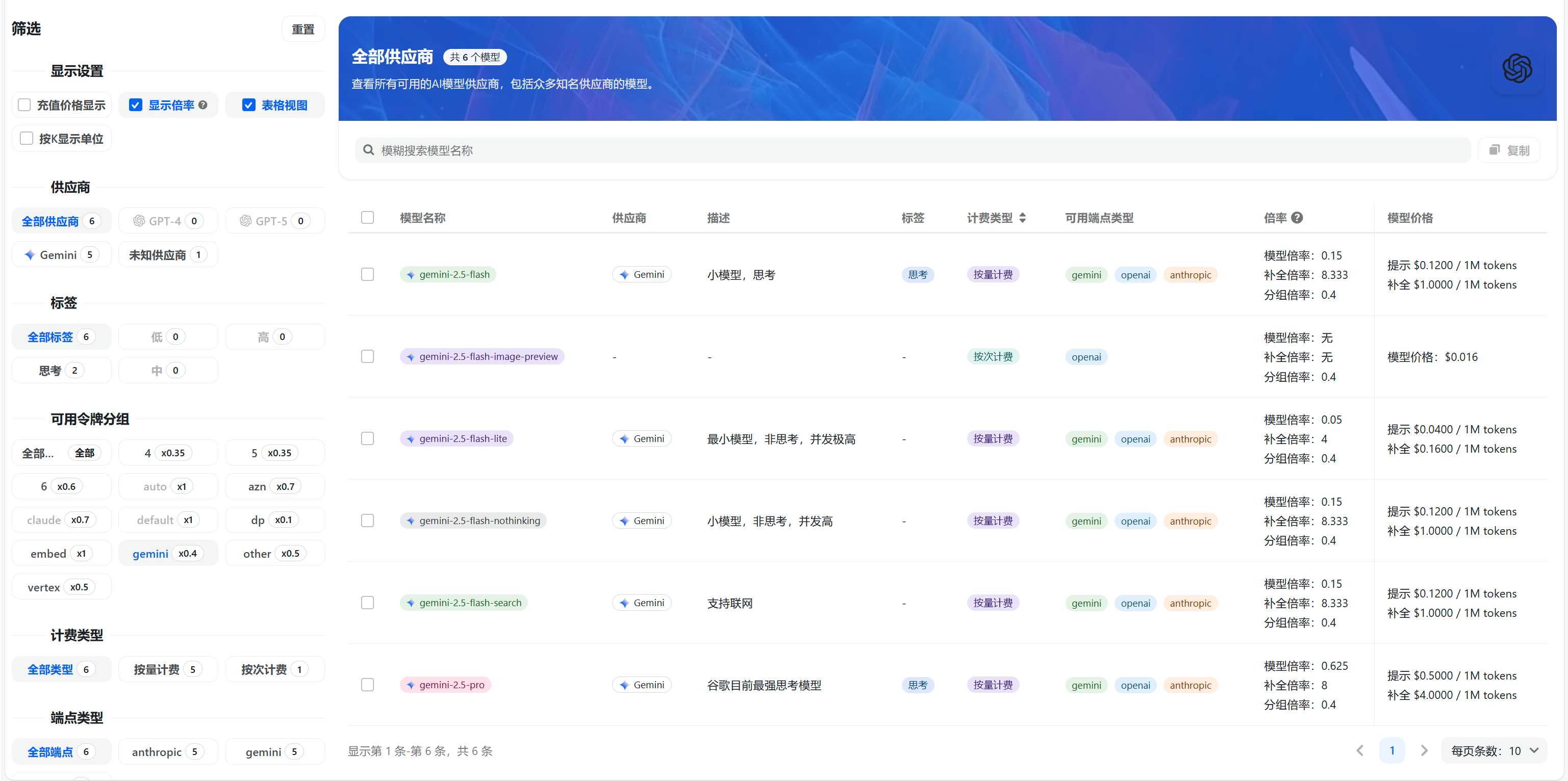
模型广场查看的即当前价格,以gemini-2.5-flash为例:
该模型官方模型倍率是:0.15,官方输入价格是:0.3$/1M,补全倍率:8.333,官方输出价格是:2.5$/1M
显示倍率:倍率为1代表模型的官方价格为2$/M,倍率可以直观比较各种模型的相对价格,如果你不清楚如何计算,请关闭显示倍率。
补全倍率:由官方输出价格除官方输入价格得出,如果你不清楚如何计算,请忽略。
分组倍率:该值代表本站相对官方的折扣,日志会在计算完官方价格后再乘分组倍率,两者相乘就是使用本站的价格。
gemini的分组倍率为0.4,由于全站充值1元=1刀,就代表gemini模型0.4元/刀,官方价格0.3$/M*分组倍率0.4=0.12$/M,本站显示的模型价格就是0.12$/M,本站显示的模型价格$其实也可以改写成元,所以本站gemini-2.5-flash的输入是0.12元/M。
分组倍率0.4,折扣实际上是0.4/7.2,即约为官方价格的5.5%
充值价格显示:无需勾选,由于全站充值1元=1刀,无论勾不勾选,货币单位选$还是¥,显示的价格都是一样的,将$看成¥就是人民币价格。价格清晰,无任何套路。
按K显示单位:1M tokens=1000K tokens,一些站点按K显示会显得价格便宜。

上面价格的提示0.12$/M其实就是0.12元/M,日志计算出来的$0.001638其实就是0.001638元。
市场价浮动较大时分组倍率可能会调整,不支持囤货。如有调价,会在控制台-数据看板-系统公告 显示。
充值
在钱包可自助24小时在线充值,充值最低金额为1元。1元兑换本平台1$。
由于对接在线充值需5%手续费,实际在线充值是1.05元兑换本平台1$。
(正常1分钟以内即可到账,没到账请先等待5分钟,还没有后再联系客服)
100元及以上可联系客服充值免手续费(100元=100刀)
联系方式wx uscnhao QQ3323203640
退款:当所需模型价格上涨或不可用时,可申请退款。注册赠送1$额度不可退款,在线充值5%手续费不可退款。
在线使用
先点侧边栏的令牌,再点令牌的聊天,本站提供多个前端可选择
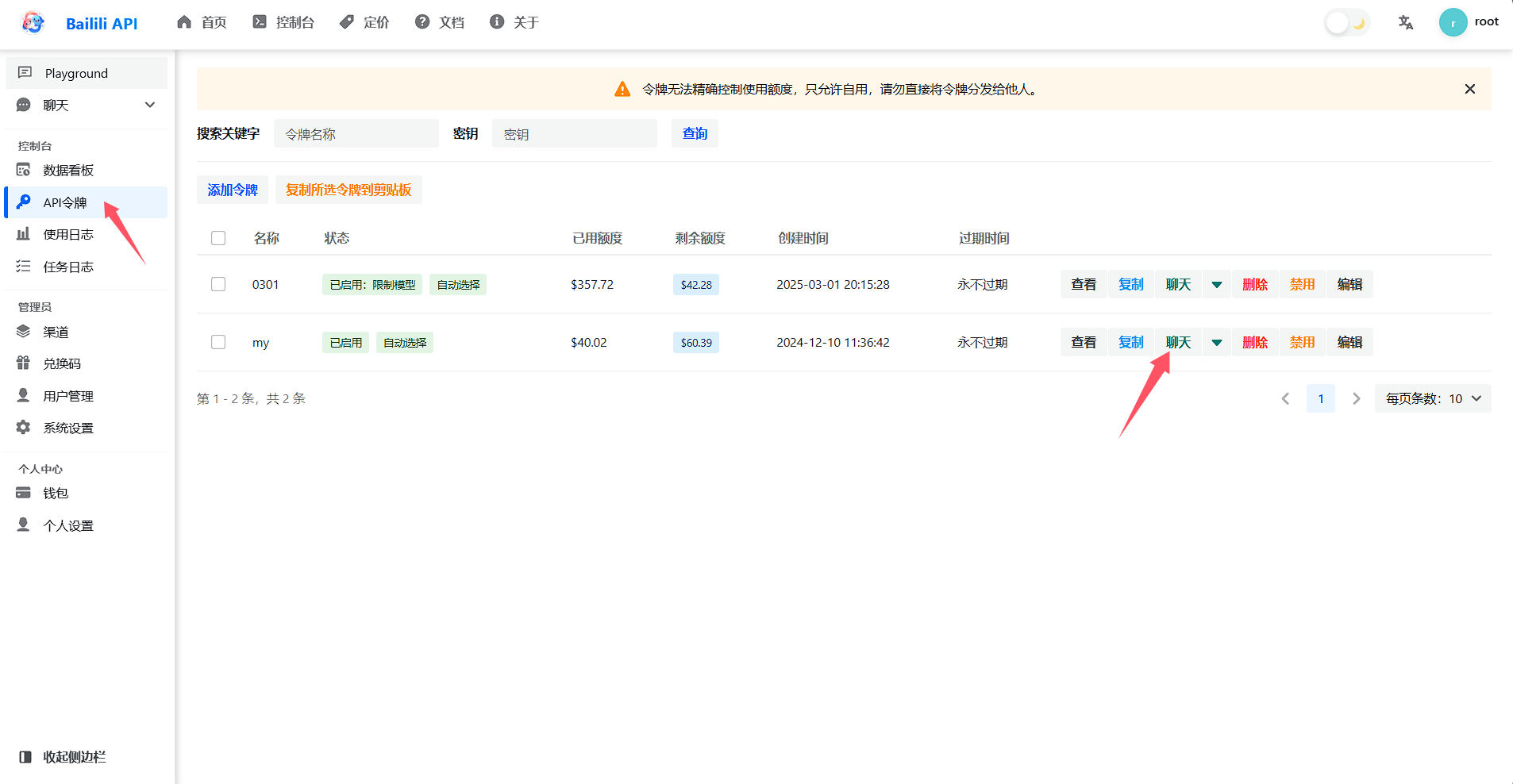
不要用playground,因为playground未适配部分模型的一些参数,容易报错
不要用侧边栏的,因为网络路由不稳定,请始终点击令牌后点击令牌的聊天,进入新网站 https://chat.bailili.top/#/ 后对话
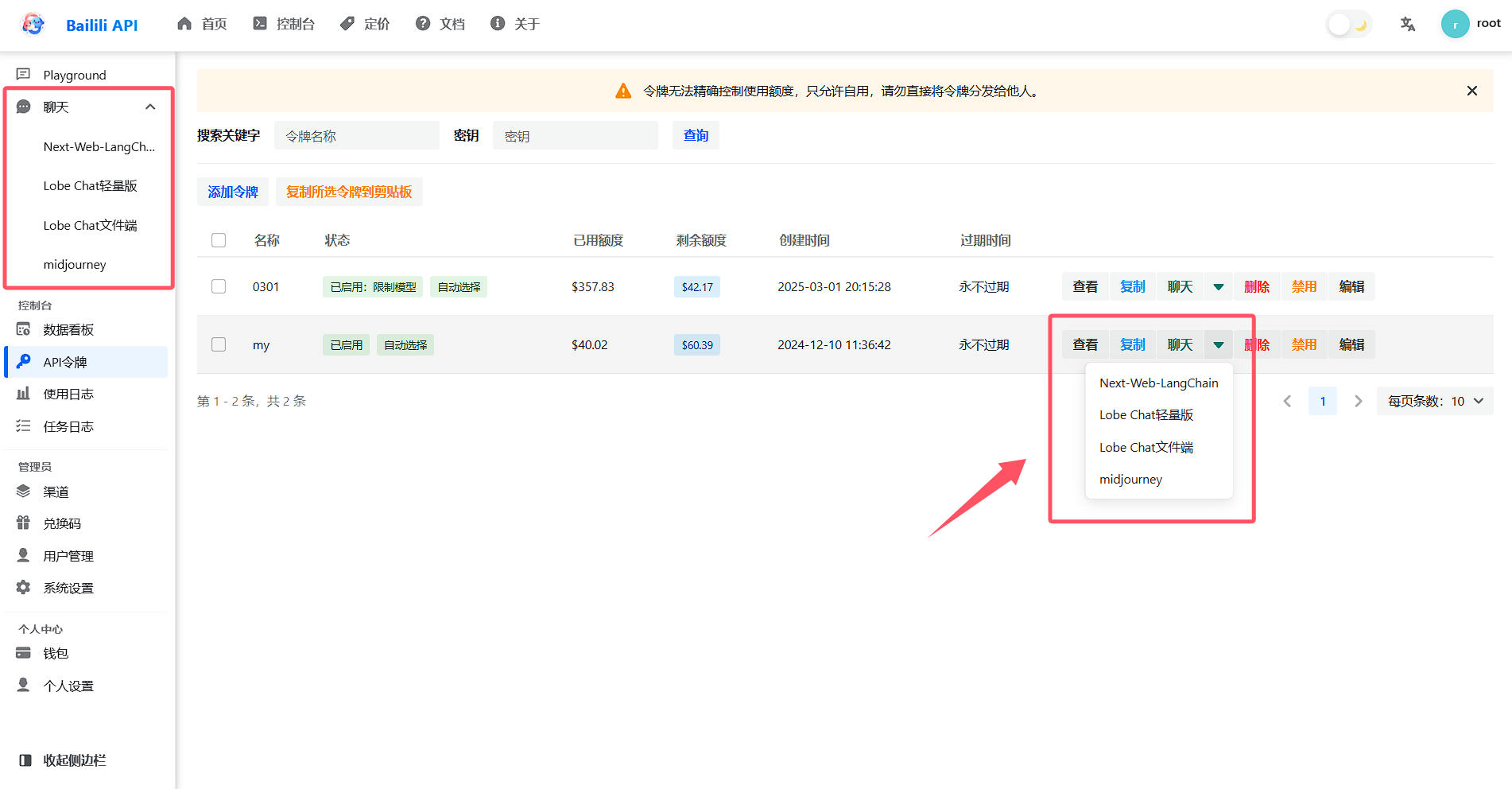
可以选择不同的前端:
Next-Web-Langchain:默认前端,点击即可使用,无需额外配置,支持插件调用。相比于原版nextchat,功能更多,无广告
Lobelite文件端:支持上传PDF文件
Next-Web-Langchain
可选操作
可以适量调整上下文长度,和是否开启压缩历史消息(压缩时也会产生请求)
可以回到最上方选择是否自动生成标题(自动生成标题也会产生请求)
这些请求都可以在api网站的日志看到
改完所有设置后会自动保存,直接右上角叉掉就可以开始对话
插件模式画图
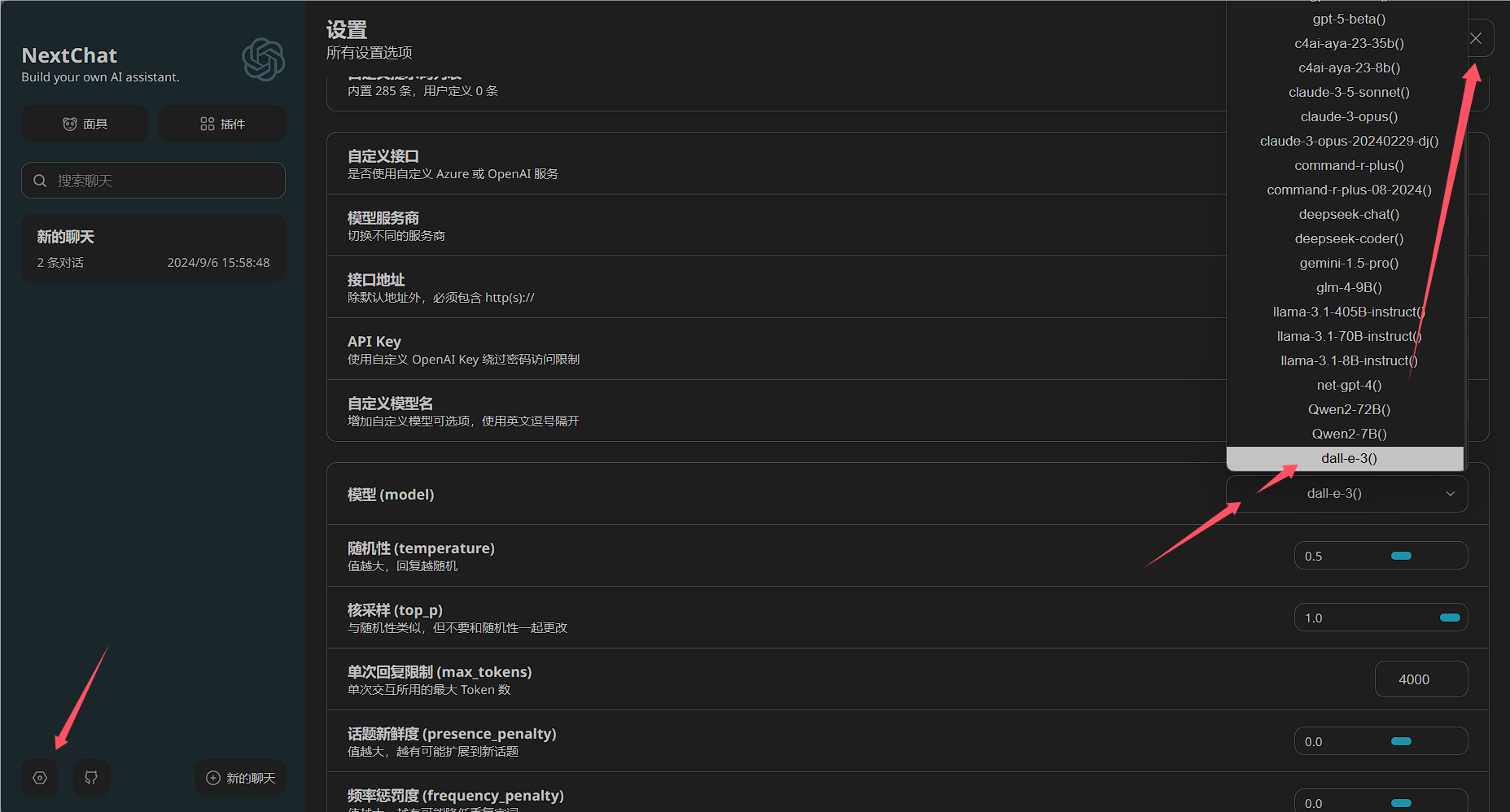
点击设置,选择dall-e-3,叉掉
选择模型,选择gpt-4o,打开插件模式
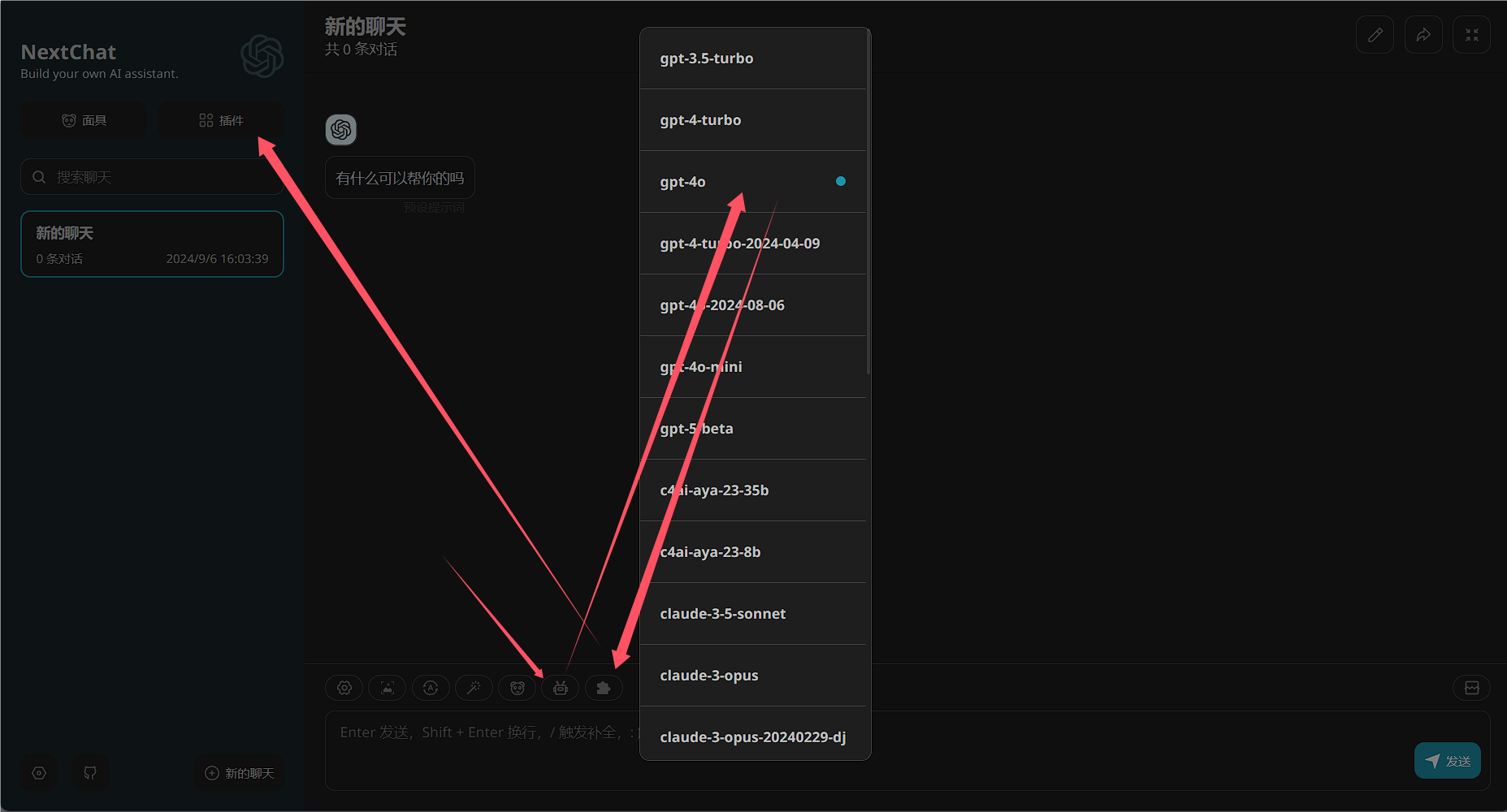
开启dalle插件

Lobe文件端
Lobe文件端:支持文件解析,文件存储,进入后先左上角使用github登录,然后点左上角应用设置-AI服务商-OpenaAI,API Key自己复制,API 代理地址填写 https://api.bailili.top/v1
获取模型列表,开启所需模型
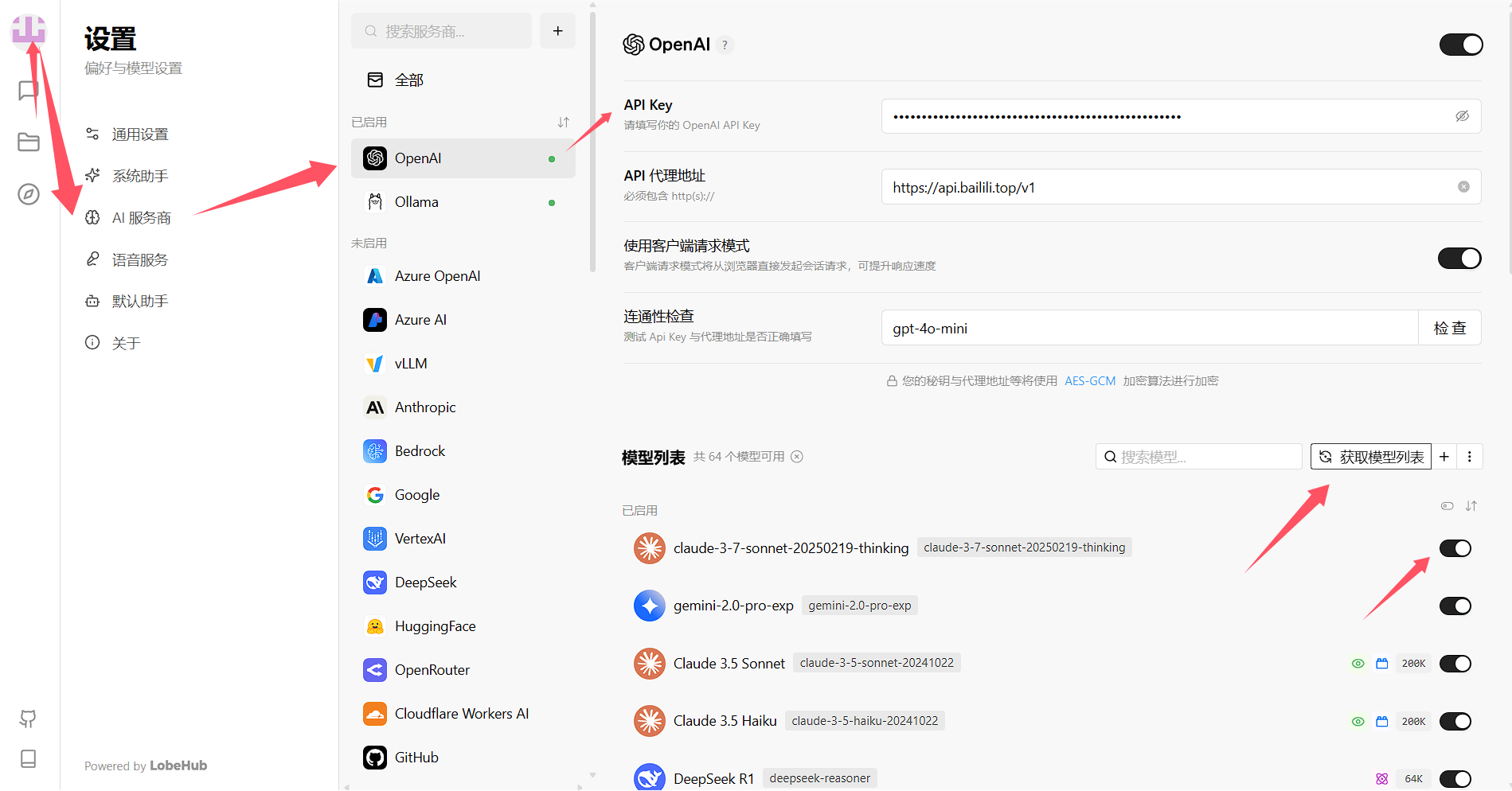 语言模型填入key,获取模型列表,按需填入模型后即可对话(会使用嵌入模型,产生极小额外消费)
语言模型填入key,获取模型列表,按需填入模型后即可对话(会使用嵌入模型,产生极小额外消费)
mj实时语音:进去后手动设置 url 为 https://new.bailili.top ,key自己复制,然后点语音
故障排除
如果报错,请检查排除下面的情况:
1. 你的令牌没有额度了,请给令牌分配足够的额度
2. 你的钱包没余额了,请及时充值,个人设置里可设置额度预警阈值并发邮件提醒
怀疑API无法使用时,使用playground测试,选择auto分组,若能聊天,检查你的API配置。若报错,带报错信息+模型名称进群反馈
模型介绍
gpt-5
gpt-5系列包括以下模型,其中高亮较为常用。
gpt-5 会自己决定是否思考,gpt-5-chat 不思考,开启思考需传参"reasoning_effort":"minimal low medium high",或直接请求带后缀模型
聊天时,mini和nano模型需要关闭temperature和top_p,或设置为1(官方限制)
输出思考内容
官方文档:API Reference - OpenAI API
示例:
POST:https://api.bailili.top/v1/responses
{
"model": "gpt-5",
"input": "∫(1/x+1) dx",
"reasoning": {
"summary": "detailed"
}
}
对于gpt-5 和长难思考题,建议使用ip,使用非流请求
输入多,时间长的请求,官方流式返回有问题,会空回复,建议流式
流式首字/非流超过100s的请求,使用域名,cf会拦截,私聊管理获取中转ip
超长回复测试题:∫(1/x^5+1) dx
搜索gpt-5的使用日志:gpt-5%
newapi二次转发建议环境变量设置STREAMING_TIMEOUT=1000
gemini
除了上面三gemini-2.5-flash-nothinking
问:更新了2.5Pro之后,输出截断更多了,似乎是内容审查导致的?怎么解决?
答:本站用newapi进行中转后,已默认设置为最低审查。但是,就算关闭了所有可以关闭的审查,谷歌仍然保留了csam等“基础审核”,且不可关闭,因此截断内容/空回复的现象仍然会存在,使用非流请求对输出截断有一定的缓解。
参考Gemini 模型 ; API速率限制 ;GCP速率限制;Gemini 思考;图片生成;Gemini 2.5 Pro on Vertex AI;输入文件;
Google Cloud Next 2025;Google Cloud Service Health
查看API可用模型curl -X GET 'https://generativelanguage.googleapis.com/v1beta/models?key='
API调用
base url
请根据程序的参考示例尝试下面的地址:
本站api所有模型均为标准openai接口,需自行在令牌页生成key,然后将接口替换成本站:
https://api.openai.com -> https://api.bailili.top
https://api.openai.com/ -> https://api.bailili.top/
https://api.openai.com/v1 -> https://api.bailili.top/v1
https://api.openai.com/v1/chat/completions -> https://api.bailili.top/v1/chat/completions
请注意,很多网站要填的是第一行,无需加域名结尾的/
key
key就是令牌,请始终生成auto分组的key以访问所有模型
请 妥善保管 你的 key,不要将key填在不明的网站和应用内,以防被他人刷取费用!如有需要,可给令牌设置额度防止大额损失
令牌无法精确控制使用额度,只允许自用,请勿直接将令牌分发给他人,若因此造成的损失,本站不负任何责任
令牌的额度仅用于限制令牌本身的最大额度使用量,实际使用时还受到账户余额限制
当令牌设为无限额度时,仅账户余额限制令牌使用额度
站点选择
使用域名时,如果有超过100的日志,前端却没有收到或显示524,是因为cf连接超过100就关闭了
o1-mini,claude3-7等模型在长文本下思考时间较长,可能经常超过100s,若有上述场景,建议使用流式请求,或联系客服使用ip
api接口基础教程
聊天请求:聊天接口(OpenAI格式通用) - AI模型API中文文档
嵌入请求:创建嵌入 - API reference
本站支持openai接口调用所有模型,支持claude原生格式调用claude,暂不支持gemini原生格式调用gemini
假如终端应用给出openai接口和gemini接口,应选择openai接口接入本站gemini模型
接入newapi二次分发
Calcium-Ion/new-api-horizon: 特性版 - 基于New API开发的增强版本,专注于高性能
本站使用horizon版本,也推荐下游使用
部署后,添加渠道,代理地址填写 https://api.bailili.top,密钥自己复制,即可接入
接入claude-3-7-sonnet-20250219
1.claude官方格式接入thinking
官方文档:Building with extended thinking - Anthropic
POST:https://api.bailili.top/v1/messages
{
"model": "claude-3-7-sonnet-20250219",
"max_tokens": 20000,
"thinking": {
"type": "enabled",
"budget_tokens": 16000
},
"messages": [
{
"role": "user",
"content": "1/(1+x^3)的不定积分"
}
]
}claude原生格式接入claude-3-7-sonnet-20250219不再赘述,上面的格式删掉"thinking"即可
{
"id": "msg_01LkSHA4Y6mWswxpyxRn7z7x",
"type": "message",
"role": "assistant",
"model": "claude-3-7-sonnet-20250219",
"content": [
{
"type": "thinking",
"thinking": "I need to find the indefinite integral of $\\frac{1}{1+x^3}$.\n\nThis is a non-trivial integral. Let's try to do a partial fraction decomposition. \n\nWe have $1 + x^3 = 0$ at $x = -1$.\n\nActually, let's factor $1 + x^3$. We have \n\\begin{align}\n1 + x^3 &= 1 + x^3\\\\\n\\end{align}\n\nLet's think more carefully. We know that if $x^3 = -1$, then $x = -1$ is one root. The other roots are complex, and we can find them by factoring.\n\n\\begin{align}\n1 + x^3 &= (x + 1)(x^2 - x + 1)\n\\end{align}\n\nWe can verify this: $(x+1)(x^2 - x + 1) = x^3 - x^2 + x + x^2 - x + 1 = x^3 + 1$.\n\nNow, we can do partial fraction decomposition.\n\\begin{align}\n\\frac{1}{1+x^3} &= \\frac{1}{(x+1)(x^2 - x + 1)}\\\\\n&= \\frac{A}{x+1} + \\frac{Bx + C}{x^2 - x + 1}\n\\end{align}\n\nMultiplying both sides by $(x+1)(x^2 - x + 1)$, we get \n\\begin{align}\n1 &= A(x^2 - x + 1) + (Bx + C)(x+1)\\\\\n&= A(x^2 - x + 1) + Bx(x+1) + C(x+1)\\\\\n&= A(x^2 - x + 1) + Bx^2 + Bx + Cx + C\\\\\n&= Ax^2 - Ax + A + Bx^2 + Bx + Cx + C\\\\\n&= (A+B)x^2 + (-A+B+C)x + (A+C)\n\\end{align}\n\nComparing with the coefficients of the left-hand side (which is just 1), we get \n\\begin{align}\nA + B &= 0\\\\\n-A + B + C &= 0\\\\\nA + C &= 1\n\\end{align}\n\nFrom the first equation, we have $B = -A$. Substitute into the second equation.\n\\begin{align}\n-A - A + C &= 0\\\\\n\\Rightarrow -2A + C &= 0\\\\\n\\Rightarrow C &= 2A\n\\end{align}\n\nSubstitute into the third equation.\n\\begin{align}\nA + 2A &= 1\\\\\n\\Rightarrow 3A &= 1\\\\\n\\Rightarrow A &= \\frac{1}{3}\n\\end{align}\n\nNow we can find the other variables.\n\\begin{align}\nB &= -A = -\\frac{1}{3}\\\\\nC &= 2A = \\frac{2}{3}\n\\end{align}\n\nSo, we have \n\\begin{align}\n\\frac{1}{1+x^3} &= \\frac{1/3}{x+1} + \\frac{-x/3 + 2/3}{x^2 - x + 1}\\\\\n&= \\frac{1}{3(x+1)} + \\frac{-x + 2}{3(x^2 - x + 1)}\n\\end{align}\n\nNow, we need to compute the integrals of each term.\n\nFor the first term, $\\frac{1}{3(x+1)}$, the integral is $\\frac{1}{3}\\ln|x+1| + C_1$.\n\nFor the second term, $\\frac{-x + 2}{3(x^2 - x + 1)}$, let's simplify.\n\\begin{align}\n\\frac{-x + 2}{3(x^2 - x + 1)} &= \\frac{-x + 1/2 + 3/2}{3(x^2 - x + 1)}\\\\\n&= \\frac{-(x - 1/2)}{3(x^2 - x + 1)} + \\frac{3/2}{3(x^2 - x + 1)}\\\\\n&= \\frac{-(x - 1/2)}{3(x^2 - x + 1)} + \\frac{1/2}{(x^2 - x + 1)}\n\\end{align}\n\nNow, let's consider each new term separately.\n\nFor $\\frac{-(x - 1/2)}{3(x^2 - x + 1)}$, we note that the derivative of $x^2 - x + 1$ is $2x - 1 = 2(x - 1/2)$. So, \n\\begin{align}\n\\frac{-(x - 1/2)}{3(x^2 - x + 1)} &= \\frac{-1}{6} \\cdot \\frac{2(x - 1/2)}{(x^2 - x + 1)}\\\\\n&= \\frac{-1}{6} \\cdot \\frac{d}{dx}[\\ln(x^2 - x + 1)]\n\\end{align}\n\nThe integral of this is $\\frac{-1}{6}\\ln(x^2 - x + 1) + C_2$.\n\nActually I'm making an error above because I'm getting confused with signs. Let's redo the calculation in a cleaner way.\n\nLet's reconsider the partial fraction decomposition.\nWe have:\n\\begin{align}\n\\frac{1}{1+x^3} &= \\frac{1}{(x+1)(x^2 - x + 1)}\\\\\n&= \\frac{A}{x+1} + \\frac{Bx + C}{x^2 - x + 1}\n\\end{align}\n\nMultiplying both sides by $(x+1)(x^2 - x + 1)$, we get \n\\begin{align}\n1 &= A(x^2 - x + 1) + (Bx + C)(x+1)\\\\\n\\end{align}\n\nWhen $x = -1$, we get:\n\\begin{align}\n1 &= A(1 + 1 + 1)\\\\\n&= 3A\\\\\n\\Rightarrow A &= \\frac{1}{3}\n\\end{align}\n\nTo find $B$ and $C$, let's expand the equation:\n\\begin{align}\n1 &= A(x^2 - x + 1) + (Bx + C)(x+1)\\\\\n&= \\frac{1}{3}(x^2 - x + 1) + (Bx + C)(x+1)\\\\\n&= \\frac{1}{3}x^2 - \\frac{1}{3}x + \\frac{1}{3} + Bx^2 + Bx + Cx + C\\\\\n&= (\\frac{1}{3} + B)x^2 + (-\\frac{1}{3} + B + C)x + (\\frac{1}{3} + C)\n\\end{align}\n\nComparing coefficients with the left-hand side:\n\\begin{align}\n\\frac{1}{3} + B &= 0\\\\\n-\\frac{1}{3} + B + C &= 0\\\\\n\\frac{1}{3} + C &= 1\n\\end{align}\n\nFrom the first equation, $B = -\\frac{1}{3}$.\nFrom the third equation, $C = \\frac{2}{3}$.\n\nLet's check the second equation:\n\\begin{align}\n-\\frac{1}{3} + (-\\frac{1}{3}) + \\frac{2}{3} &= 0\\\\\n-\\frac{1}{3} - \\frac{1}{3} + \\frac{2}{3} &= 0\\\\\n\\frac{-2 + 2}{3} &= 0\\\\\n0 &= 0\n\\end{align}\n\nGreat, so it checks out.\n\nSo, we have:\n\\begin{align}\n\\frac{1}{1+x^3} &= \\frac{1/3}{x+1} + \\frac{-x/3 + 2/3}{x^2 - x + 1}\\\\\n&= \\frac{1}{3(x+1)} + \\frac{-x/3 + 2/3}{x^2 - x + 1}\n\\end{align}\n\nNow, we need to integrate each term.\n\nFor the first term, $\\frac{1}{3(x+1)}$, the integral is $\\frac{1}{3}\\ln|x+1| + C_1$.\n\nFor the second term, $\\frac{-x/3 + 2/3}{x^2 - x + 1}$, let's split it:\n\\begin{align}\n\\frac{-x/3 + 2/3}{x^2 - x + 1} &= \\frac{-x/3}{x^2 - x + 1} + \\frac{2/3}{x^2 - x + 1}\n\\end{align}\n\nFor $\\frac{-x/3}{x^2 - x + 1}$, we can rewrite:\n\\begin{align}\n\\frac{-x/3}{x^2 - x + 1} &= \\frac{-1}{3} \\cdot \\frac{x}{x^2 - x + 1}\n\\end{align}\n\nThe derivative of $x^2 - x + 1$ is $2x - 1$. We can't directly use substitution.\n\nLet me rewrite the term from the beginning:\n\\begin{align}\n\\frac{-x/3 + 2/3}{x^2 - x + 1} &= \\frac{-x/3 + 1/6 + 1/2}{x^2 - x + 1}\\\\\n&= \\frac{-x/3 + 1/6}{x^2 - x + 1} + \\frac{1/2}{x^2 - x + 1}\n\\end{align}\n\nNotice that $-x/3 + 1/6 = -(x/3 - 1/6) = -\\frac{1}{3}(x - 1/2)$. And also notice that $\\frac{d}{dx}(x^2 - x + 1) = 2x - 1 = 2(x - 1/2)$.\n\nSo, we can rewrite:\n\\begin{align}\n\\frac{-x/3 + 1/6}{x^2 - x + 1} &= \\frac{-\\frac{1}{3}(x - 1/2)}{x^2 - x + 1}\\\\\n&= \\frac{-\\frac{1}{3} \\cdot \\frac{1}{2} \\cdot 2(x - 1/2)}{x^2 - x + 1}\\\\\n&= -\\frac{1}{6} \\cdot \\frac{2(x - 1/2)}{x^2 - x + 1}\\\\\n&= -\\frac{1}{6} \\cdot \\frac{\\frac{d}{dx}(x^2 - x + 1)}{x^2 - x + 1}\\\\\n&= -\\frac{1}{6} \\cdot \\frac{d}{dx}[\\ln(x^2 - x + 1)]\n\\end{align}\n\nThe integral of this is $-\\frac{1}{6}\\ln(x^2 - x + 1) + C_2$.\n\nFor $\\frac{1/2}{x^2 - x + 1}$, we can complete the square in the denominator:\n\\begin{align}\nx^2 - x + 1 &= x^2 - x + \\frac{1}{4} + 1 - \\frac{1}{4}\\\\\n&= (x - \\frac{1}{2})^2 + \\frac{3}{4}\n\\end{align}\n\nSo,\n\\begin{align}\n\\frac{1/2}{x^2 - x + 1} &= \\frac{1/2}{(x - \\frac{1}{2})^2 + \\frac{3}{4}}\\\\\n&= \\frac{1/2}{(x - \\frac{1}{2})^2 + (\\frac{\\sqrt{3}}{2})^2}\n\\end{align}\n\nWe can use the arctangent formula here: $\\int \\frac{1}{x^2 + a^2}dx = \\frac{1}{a}\\arctan(\\frac{x}{a}) + C$.\n\nApplying this to our integral:\n\\begin{align}\n\\int \\frac{1/2}{(x - \\frac{1}{2})^2 + (\\frac{\\sqrt{3}}{2})^2}dx &= \\frac{1/2}{\\frac{\\sqrt{3}}{2}}\\arctan\\left(\\frac{x - \\frac{1}{2}}{\\frac{\\sqrt{3}}{2}}\\right) + C_3\\\\\n&= \\frac{1}{\\sqrt{3}}\\arctan\\left(\\frac{2(x - \\frac{1}{2})}{\\sqrt{3}}\\right) + C_3\\\\\n&= \\frac{1}{\\sqrt{3}}\\arctan\\left(\\frac{2x - 1}{\\sqrt{3}}\\right) + C_3\n\\end{align}\n\nCombining all the pieces, the indefinite integral of $\\frac{1}{1+x^3}$ is:\n\\begin{align}\n\\int \\frac{1}{1+x^3}dx &= \\frac{1}{3}\\ln|x+1| - \\frac{1}{6}\\ln(x^2 - x + 1) + \\frac{1}{\\sqrt{3}}\\arctan\\left(\\frac{2x - 1}{\\sqrt{3}}\\right) + C\n\\end{align}\n\nOk actually I'm getting a bit confused with all the different terms. Let me try a different approach from the beginning.\n\nWe have the integral:\n\\begin{align}\n\\int \\frac{1}{1+x^3}dx\n\\end{align}\n\nWe know:\n\\begin{align}\n1 + x^3 &= (x+1)(x^2 - x + 1)\n\\end{align}\n\nNow, let's do a proper partial fraction decomposition:\n\\begin{align}\n\\frac{1}{1+x^3} &= \\frac{1}{(x+1)(x^2 - x + 1)}\\\\\n&= \\frac{A}{x+1} + \\frac{Bx + C}{x^2 - x + 1}\n\\end{align}\n\nWhen $x = -1$:\n\\begin{align}\n1 &= A \\cdot ((-1)^2 - (-1) + 1)\\\\\n&= A \\cdot (1 + 1 + 1)\\\\\n&= 3A\\\\\n\\Rightarrow A &= \\frac{1}{3}\n\\end{align}\n\nNow, let's find $B$ and $C$:\n\\begin{align}\n\\frac{1}{(x+1)(x^2 - x + 1)} &= \\frac{1/3}{x+1} + \\frac{Bx + C}{x^2 - x + 1}\n\\end{align}\n\nMultiply both sides by $(x+1)(x^2 - x + 1)$:\n\\begin{align}\n1 &= \\frac{1}{3}(x^2 - x + 1) + (Bx + C)(x+1)\\\\\n&= \\frac{1}{3}x^2 - \\frac{1}{3}x + \\frac{1}{3} + Bx^2 + Bx + Cx + C\n\\end{align}\n\nGrouping terms:\n\\begin{align}\n1 &= \\left(\\frac{1}{3} + B\\right)x^2 + \\left(-\\frac{1}{3} + B + C\\right)x + \\left(\\frac{1}{3} + C\\right)\n\\end{align}\n\nComparing coefficients:\n\\begin{align}\n\\frac{1}{3} + B &= 0\\\\\n-\\frac{1}{3} + B + C &= 0\\\\\n\\frac{1}{3} + C &= 1\n\\end{align}\n\nFrom the first equation, $B = -\\frac{1}{3}$.\nFrom the third equation, $C = \\frac{2}{3}$.\n\nSo:\n\\begin{align}\n\\frac{1}{1+x^3} &= \\frac{1/3}{x+1} + \\frac{-x/3 + 2/3}{x^2 - x + 1}\n\\end{align}\n\nLet's integrate the terms separately.\n\nFor the first term:\n\\begin{align}\n\\int \\frac{1/3}{x+1}dx &= \\frac{1}{3}\\ln|x+1| + C_1\n\\end{align}\n\nFor the second term, let's rewrite:\n\\begin{align}\n\\frac{-x/3 + 2/3}{x^2 - x + 1} &= \\frac{-x/3 + 1/6 + 1/2}{x^2 - x + 1}\n\\end{align}\n\nLet's consider:\n\\begin{align}\n\\frac{-x/3 + 1/6}{x^2 - x + 1} &= \\frac{-\\frac{1}{3}(x - 1/2)}{x^2 - x + 1}\n\\end{align}\n\nThe derivative of $x^2 - x + 1$ is $2x - 1 = 2(x - 1/2)$. So:\n\\begin{align}\n\\frac{-\\frac{1}{3}(x - 1/2)}{x^2 - x + 1} &= -\\frac{1}{6} \\cdot \\frac{2(x - 1/2)}{x^2 - x + 1}\\\\\n&= -\\frac{1}{6} \\cdot \\frac{d}{dx}[\\ln(x^2 - x + 1)]\n\\end{align}\n\nThe integral of this is:\n\\begin{align}\n\\int -\\frac{1}{6} \\cdot \\frac{d}{dx}[\\ln(x^2 - x + 1)]dx &= -\\frac{1}{6}\\ln(x^2 - x + 1) + C_2\n\\end{align}\n\nFor the term $\\frac{1/2}{x^2 - x + 1}$, we can complete the square in the denominator:\n\\begin{align}\nx^2 - x + 1 &= (x - \\frac{1}{2})^2 + \\frac{3}{4}\n\\end{align}\n\nSo:\n\\begin{align}\n\\frac{1/2}{x^2 - x + 1} &= \\frac{1/2}{(x - \\frac{1}{2})^2 + \\frac{3}{4}}\\\\\n&= \\frac{1/2}{(x - \\frac{1}{2})^2 + (\\frac{\\sqrt{3}}{2})^2}\n\\end{align}\n\nUsing the formula for the arctangent:\n\\begin{align}\n\\int \\frac{1/2}{(x - \\frac{1}{2})^2 + (\\frac{\\sqrt{3}}{2})^2}dx &= \\frac{1/2}{\\frac{\\sqrt{3}}{2}}\\arctan\\left(\\frac{x - \\frac{1}{2}}{\\frac{\\sqrt{3}}{2}}\\right) + C_3\\\\\n&= \\frac{1}{\\sqrt{3}}\\arctan\\left(\\frac{2(x - \\frac{1}{2})}{\\sqrt{3}}\\right) + C_3\\\\\n&= \\frac{1}{\\sqrt{3}}\\arctan\\left(\\frac{2x - 1}{\\sqrt{3}}\\right) + C_3\n\\end{align}\n\nCombining all the pieces, the indefinite integral of $\\frac{1}{1+x^3}$ is:\n\\begin{align}\n\\int \\frac{1}{1+x^3}dx &= \\frac{1}{3}\\ln|x+1| - \\frac{1}{6}\\ln(x^2 - x + 1) + \\frac{1}{\\sqrt{3}}\\arctan\\left(\\frac{2x - 1}{\\sqrt{3}}\\right) + C\n\\end{align}\n\nActually let's double-check because this still feels overly complicated.\n\nWe have:\n\\begin{align}\n\\frac{1}{1+x^3} &= \\frac{1/3}{x+1} + \\frac{-x/3 + 2/3}{x^2 - x + 1}\n\\end{align}\n\nThe first term's integral is straightforward:\n\\begin{align}\n\\int \\frac{1/3}{x+1}dx &= \\frac{1}{3}\\ln|x+1| + C_1\n\\end{align}\n\nLet's look closely at the second term:\n\\begin{align}\n\\frac{-x/3 + 2/3}{x^2 - x + 1}\n\\end{align}\n\nLet's create a substitution to simplify:\n\\begin{align}\nu &= x - \\frac{1}{2}\\\\\nx &= u + \\frac{1}{2}\\\\\ndx &= du\n\\end{align}\n\nThen:\n\\begin{align}\nx^2 - x + 1 &= (u + \\frac{1}{2})^2 - (u + \\frac{1}{2}) + 1\\\\\n&= u^2 + u + \\frac{1}{4} - u - \\frac{1}{2} + 1\\\\\n&= u^2 + \\frac{3}{4}\\\\\n&= u^2 + \\frac{\\sqrt{3}^2}{4}\n\\end{align}\n\nAnd:\n\\begin{align}\n-x/3 + 2/3 &= -(u + \\frac{1}{2})/3 + 2/3\\\\\n&= -u/3 - 1/6 + 2/3\\\\\n&= -u/3 + 1/2\n\\end{align}\n\nSo:\n\\begin{align}\n\\frac{-x/3 + 2/3}{x^2 - x + 1} &= \\frac{-u/3 + 1/2}{u^2 + \\frac{3}{4}}\n\\end{align}\n\nLet's split this into two fractions:\n\\begin{align}\n\\frac{-u/3 + 1/2}{u^2 + \\frac{3}{4}} &= \\frac{-u/3}{u^2 + \\frac{3}{4}} + \\frac{1/2}{u^2 + \\frac{3}{4}}\\\\\n&= -\\frac{1}{3} \\cdot \\frac{u}{u^2 + \\frac{3}{4}} + \\frac{1/2}{u^2 + \\frac{3}{4}}\n\\end{align}\n\nFor the first term, we know $\\int \\frac{u}{u^2 + a^2}du = \\frac{1}{2}\\ln(u^2 + a^2) + C$.\n\nSo:\n\\begin{align}\n\\int -\\frac{1}{3} \\cdot \\frac{u}{u^2 + \\frac{3}{4}}du &= -\\frac{1}{3} \\cdot \\frac{1}{2}\\ln(u^2 + \\frac{3}{4}) + C_2\\\\\n&= -\\frac{1}{6}\\ln(u^2 + \\frac{3}{4}) + C_2\\\\\n&= -\\frac{1}{6}\\ln(x^2 - x + 1) + C_2\n\\end{align}\n\nFor the second term, we use the arctangent formula:\n\\begin{align}\n\\int \\frac{1/2}{u^2 + \\frac{3}{4}}du &= \\frac{1/2}{\\sqrt{\\frac{3}{4}}}\\arctan\\left(\\frac{u}{\\sqrt{\\frac{3}{4}}}\\right) + C_3\\\\\n&= \\frac{1/2}{\\frac{\\sqrt{3}}{2}}\\arctan\\left(\\frac{u}{\\frac{\\sqrt{3}}{2}}\\right) + C_3\\\\\n&= \\frac{1}{\\sqrt{3}}\\arctan\\left(\\frac{2u}{\\sqrt{3}}\\right) + C_3\\\\\n&= \\frac{1}{\\sqrt{3}}\\arctan\\left(\\frac{2(x - \\frac{1}{2})}{\\sqrt{3}}\\right) + C_3\\\\\n&= \\frac{1}{\\sqrt{3}}\\arctan\\left(\\frac{2x - 1}{\\sqrt{3}}\\right) + C_3\n\\end{align}\n\nCombining all the pieces, the indefinite integral of $\\frac{1}{1+x^3}$ is:\n\\begin{align}\n\\int \\frac{1}{1+x^3}dx &= \\frac{1}{3}\\ln|x+1| - \\frac{1}{6}\\ln(x^2 - x + 1) + \\frac{1}{\\sqrt{3}}\\arctan\\left(\\frac{2x - 1}{\\sqrt{3}}\\right) + C\n\\end{align}\n\nOk now we have verified the integral, let's check once more.\n\nActually, let's use another method to check. We'll perform a direct substitution:\n\nLet $u = x - \\frac{1}{2}$, then $x = u + \\frac{1}{2}$ and $dx = du$.\n\n\\begin{align}\n\\int \\frac{1}{1+x^3}dx &= \\int \\frac{1}{1+(u + \\frac{1}{2})^3}du\\\\\n&= \\int \\frac{1}{1+u^3 + \\frac{3}{2}u^2 + \\frac{3}{4}u + \\frac{1}{8}}du\n\\end{align}\n\nThis doesn't simplify much. Let's stick with the original approach and the result we've already derived.\n\nLet's go ahead and reconfirm our result. We have:\n\\begin{align}\n\\int \\frac{1}{1+x^3}dx &= \\frac{1}{3}\\ln|x+1| - \\frac{1}{6}\\ln(x^2 - x + 1) + \\frac{1}{\\sqrt{3}}\\arctan\\left(\\frac{2x - 1}{\\sqrt{3}}\\right) + C\n\\end{align}\n\nIn fact this does check out. In summary, the indefinite integral of $\\frac{1}{1+x^3}$ is:\n\\begin{align}\n\\int \\frac{1}{1+x^3}dx &= \\frac{1}{3}\\ln|x+1| - \\frac{1}{6}\\ln(x^2 - x + 1) + \\frac{1}{\\sqrt{3}}\\arctan\\left(\\frac{2x - 1}{\\sqrt{3}}\\right) + C\n\\end{align}\n\nWhere $C$ is the constant of integration.",
"signature": "ErUBCkYIARgCIkAYU6lf2vEk6rC3hcZLah4LDEAUiKXjOTC73wCOlQBlGK7cXp72SZFmkKW8fwFvOm0Cfh/jpv9cqr39JJ8tHjzJEgx8X4sT4OrW2o9If1gaDPWPqtjwOR6pVt97aCIwDCTIt/p195x6p8rc8wBiM+sGOCzye34z35a9BCgW6DJBM+UIx6xrfLW6QENLwQXjKh1sOF5yXP+fArjouTTLaWPDfxG1OWV9bPM2/rnuZA=="
},
{
"type": "text",
"text": "# 不定积分 $\\int \\frac{1}{1+x^3} dx$\n\n首先我需要计算 $\\frac{1}{1+x^3}$ 的不定积分。这个积分需要使用部分分式分解法。\n\n## 部分分式分解\n\n第一步,对 $1+x^3$ 进行因式分解:\n$$1+x^3 = (x+1)(x^2-x+1)$$\n\n然后进行部分分式分解:\n$$\\frac{1}{1+x^3} = \\frac{A}{x+1} + \\frac{Bx+C}{x^2-x+1}$$\n\n当 $x = -1$ 时:\n$$1 = A((-1)^2-(-1)+1) = 3A \\Rightarrow A = \\frac{1}{3}$$\n\n对比系数法求解 $B$ 和 $C$:\n$$\\frac{1}{3}(x^2-x+1) + (Bx+C)(x+1) = 1$$\n\n展开并比较系数:\n$$\\frac{1}{3}x^2 - \\frac{1}{3}x + \\frac{1}{3} + Bx^2 + Bx + Cx + C = 1$$\n\n得到:\n$$\\left\\{\\begin{array}{l}\n\\frac{1}{3}+B=0 \\\\\n-\\frac{1}{3}+B+C=0 \\\\\n\\frac{1}{3}+C=1\n\\end{array}\\right.$$\n\n解得:$B = -\\frac{1}{3}$,$C = \\frac{2}{3}$。\n\n因此:\n$$\\frac{1}{1+x^3} = \\frac{1/3}{x+1} + \\frac{-x/3+2/3}{x^2-x+1}$$\n\n## 积分计算\n\n1. 对于第一项: $\\int \\frac{1/3}{x+1}dx = \\frac{1}{3}\\ln|x+1|$\n\n2. 对于第二项,将 $\\frac{-x/3+2/3}{x^2-x+1}$ 重写为:\n $$\\frac{-x/3+2/3}{x^2-x+1} = -\\frac{1}{6} \\cdot \\frac{d}{dx}[\\ln(x^2-x+1)] + \\frac{1/2}{x^2-x+1}$$\n\n (这里利用了 $\\frac{d}{dx}(x^2-x+1) = 2x-1$ 和部分分式调整)\n\n • $\\int -\\frac{1}{6} \\cdot \\frac{d}{dx}[\\ln(x^2-x+1)]dx = -\\frac{1}{6}\\ln(x^2-x+1)$\n \n • 对于 $\\frac{1/2}{x^2-x+1}$,注意到 $x^2-x+1 = (x-\\frac{1}{2})^2+\\frac{3}{4}$,所以:\n $$\\int \\frac{1/2}{x^2-x+1}dx = \\frac{1}{\\sqrt{3}}\\arctan\\left(\\frac{2x-1}{\\sqrt{3}}\\right)$$\n\n结合所有部分,最终积分为:\n$$\\int \\frac{1}{1+x^3}dx = \\frac{1}{3}\\ln|x+1| - \\frac{1}{6}\\ln(x^2-x+1) + \\frac{1}{\\sqrt{3}}\\arctan\\left(\\frac{2x-1}{\\sqrt{3}}\\right) + C$$\n\n其中 $C$ 为积分常数。"
}
],
"stop_reason": "end_turn",
"stop_sequence": null,
"usage": {
"input_tokens": 49,
"cache_creation_input_tokens": 0,
"cache_read_input_tokens": 0,
"output_tokens": 8138
}
}2.openai格式接入claude-3-7-sonnet-20250219-thinking
POST:https://api.bailili.top/v1/chat/completions
{
"model": "claude-3-7-sonnet-20250219-thinking",
"messages": [
{
"role": "user",
"content": "Hello!"
}
],
"stream": false
}{
"id": "msg_01WmWys1zZZSnsaN4juUh2oP",
"model": "claude-3-7-sonnet-20250219",
"object": "chat.completion",
"created": 1740724872,
"choices": [
{
"index": 0,
"message": {
"role": "assistant",
"content": "Hi there! It's nice to meet you. I'm an AI assistant ready to help with information, answer questions, or just chat. How are you doing today? Is there something I can help you with?",
"reasoning_content": "The human has sent a simple greeting \"Hello!\". I should respond in a friendly and welcoming manner, introducing myself and perhaps offering assistance."
},
"finish_reason": "stop"
}
],
"error": null,
"usage": {
"prompt_tokens": 37,
"completion_tokens": 84,
"total_tokens": 121,
"prompt_tokens_details": {
"cached_tokens": 0,
"text_tokens": 0,
"audio_tokens": 0,
"image_tokens": 0
},
"completion_tokens_details": {
"text_tokens": 0,
"audio_tokens": 0
}
}
}3.claude格式接入claude-3-7-sonnet-20250219-thinking
如果用户没传参就适配,传参了就不做更改
POST:https://api.bailili.top/v1/messages
{
"model": "claude-3-7-sonnet-20250219-thinking",
"max_tokens": 20000,
"messages": [
{
"role": "user",
"content": "Hello!"
}
]
}{
"id": "msg_01VPrrB6wq1nTTzLF6weGSX8",
"type": "message",
"role": "assistant",
"model": "claude-3-7-sonnet-20250219",
"content": [
{
"type": "thinking",
"thinking": "The user has sent a simple greeting \"Hello!\" I should respond in a friendly and welcoming manner, introducing myself and offering to assist them with whatever they might need.",
"signature": "EuYBCkQYAiJAhhlhT+Iu2dGnKPql4HJCRklPE6/FqB1TlNjtgCfDBRw+FCcu3eIe9T6FFrG3W01VHDARjydeIbRwISqRuidAmRIMuXkcXWsdsfvOvKOpGgzwpTy9GHIl53jRimMiMHsaX3Et+3Tq+wMRLiyB1oW8EgZ9qR5BwSbezCPRFacDbsFH29/E/gN0TFvOi2m8oypQowvfdmWEd6Bu1LePoDsNcimXCAbl46bWmiYmBK0Hh4bG0pBheOj+2aIDFxQj0UzESQ67OZ6b6gGHji+/IUmrzrzICTVfMscH3p2ZykPcvyg="
},
{
"type": "text",
"text": "Hi there! It's nice to meet you. I'm an AI assistant ready to help you with information, answer questions, or just chat. How are you doing today, and is there something specific I can help you with?"
}
],
"stop_reason": "end_turn",
"stop_sequence": null,
"usage": {
"input_tokens": 37,
"cache_creation_input_tokens": 0,
"cache_read_input_tokens": 0,
"output_tokens": 92
}
}4.newapi下游接入,并仍支持上述方法
更新至calciumion/new-api-horizon:latest(0.1.2.9.4及以后版本)接入时选择Anthropic Claude方式接入,填入两个模型名称即可
imagen-3.0-generate-002
POST:https://api.bailili.top/v1/images/generations
{
"model": "imagen-3.0-generate-002",
"prompt": "A cute baby sea otter",
"n": 1,
"size": "1024x1024"
}生成图片 | Generative AI on Vertex AI | Google Cloud
价格 | Generative AI on Vertex AI | Google Cloud
api接入chatluna
准备:已使用koishi接入QQ
QQ群282381753
安装chatluna和chatluna-openai-like-adapter
api接口填https://api.bailili.top/v1
api接入sus-chat
准备:已使用koishi接入QQ
QQ群775791760
安装sus-chat
api接口填https://api.bailili.top/v1
api接入酒馆
推荐edge浏览器进入,禁止用QQ进入
连接中转api:
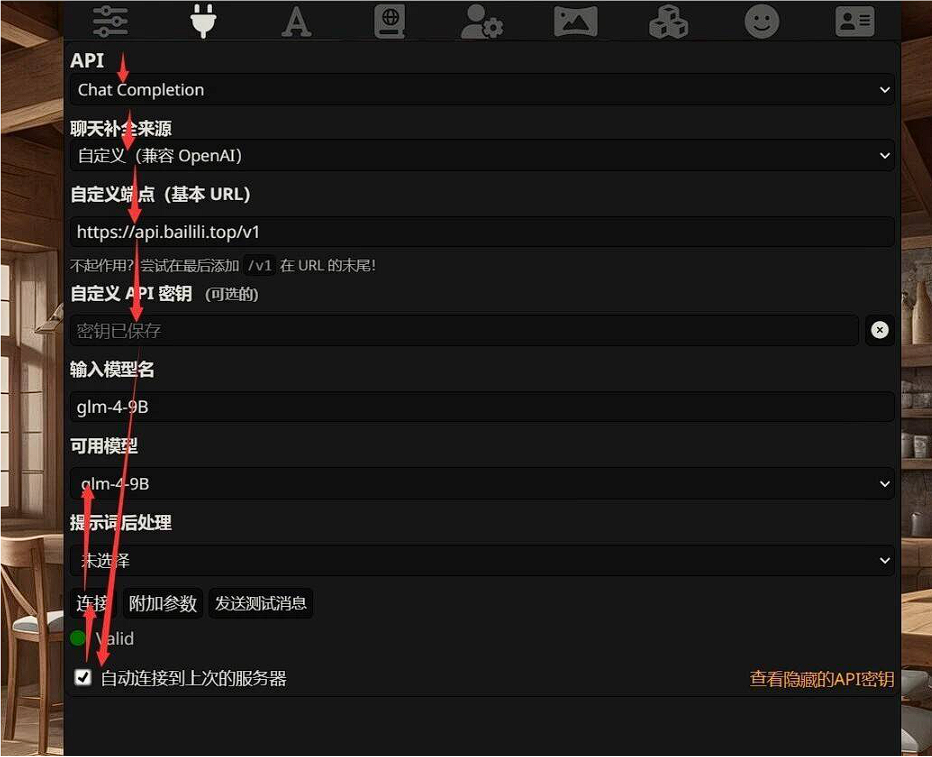
上传人格:
进入QQ群的群文件,下载:早期破限组角色卡分类包.zip
解压密码wangyue520,解压到一个找得到的地方。
进入网站,这里导入想玩的人格文件,格式就是png直接导入
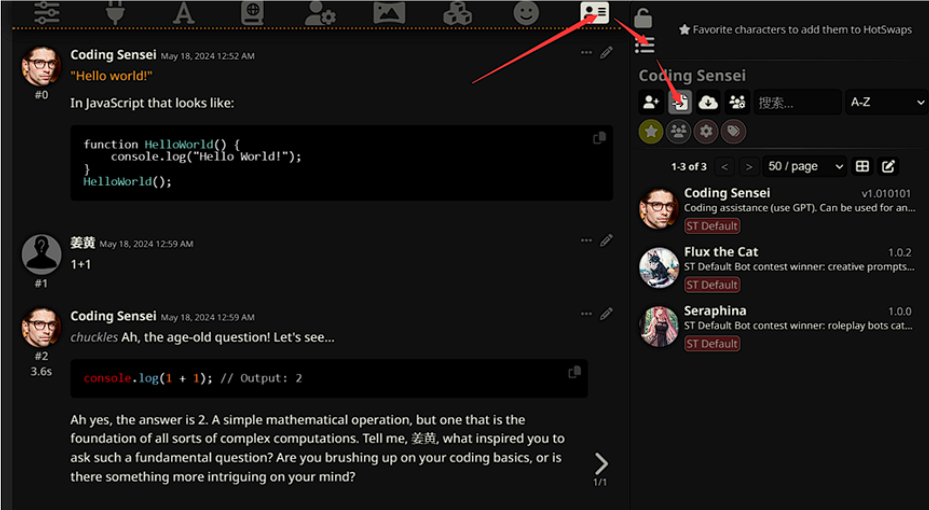
点右上角角色卡,选择角色即可对话
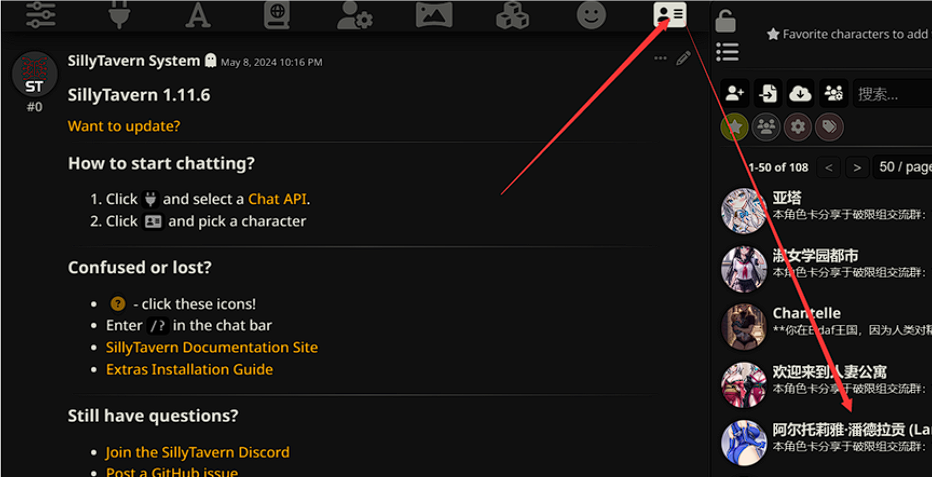
如果是手机,选完角色会出现下图,点左下角(或右下角)缝隙处开始对话
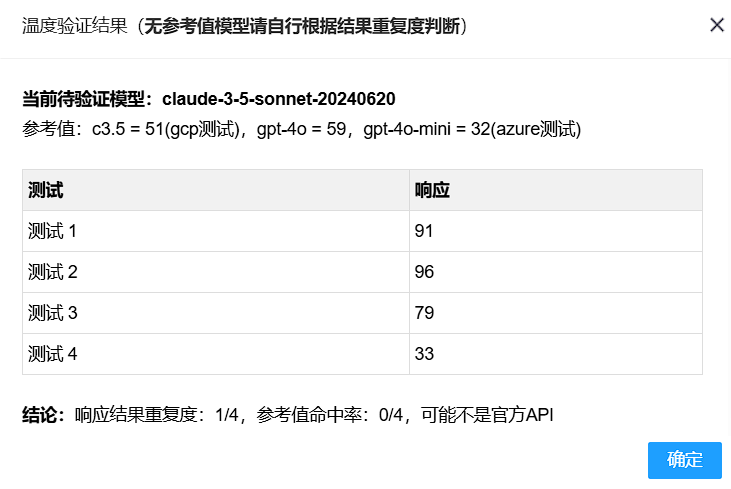
claude模型验证
claude作为模型掺假的重灾区,各种逆向掺假的低价渠道层出不穷,逆向会出现文本截断,其他来源不明的渠道回复质量更无法保证
本站坚持并保证使用官方api,保证回复质量,可自行进行对话验证和温度验证
对话验证
区分claude3-7官方/逆向方法:
询问对方是claude几-几?逆向会说自己是3-7,官api会说自己是3-opus(推测3-7为3-opus升级而来)
温度验证
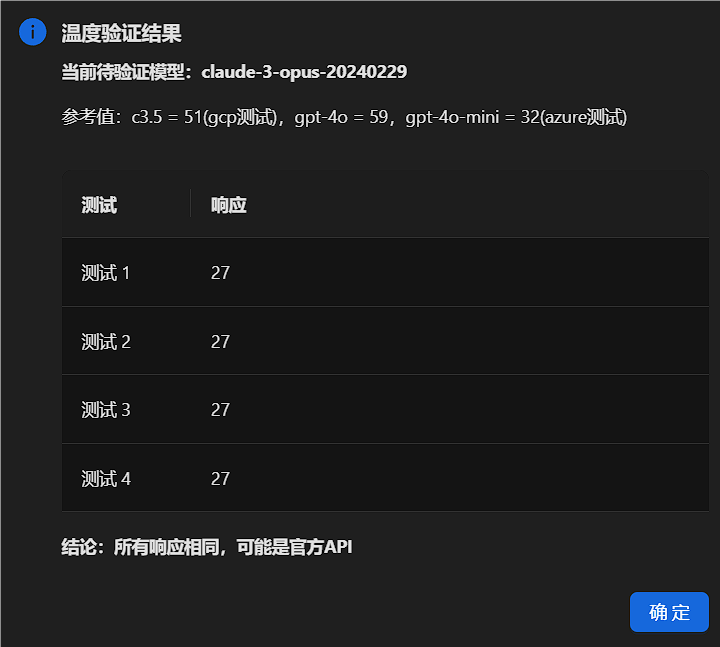
模型鉴定网站:API CHECK(防君子不防小人)
claude-sonnet-4-20250514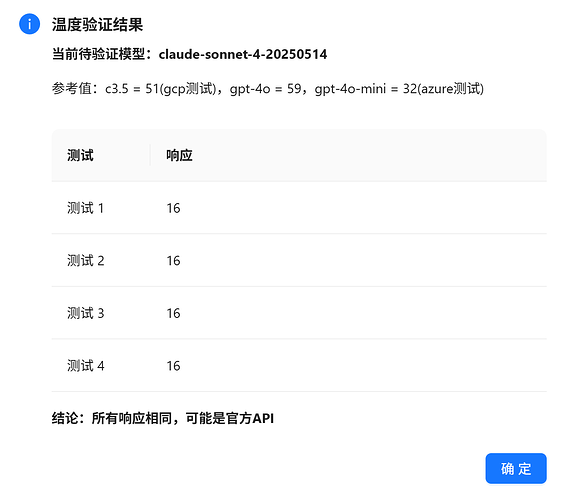
claude-sonnet-4-20250514-thinking
4次测试结果比较随机,但大部分还是55
claude-opus-4-20250514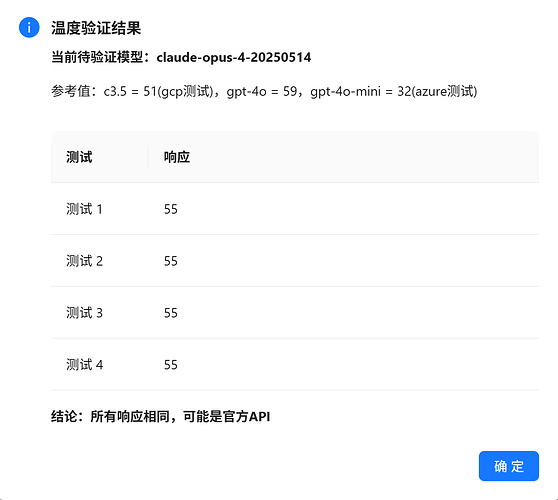
claude-opus-4-20250514-thinking
4次测试结果比较随机,但大部分还是55
使用以上网站进行claude-3-7-sonnet-20250219温度验证,本站符合官方key参考响应:
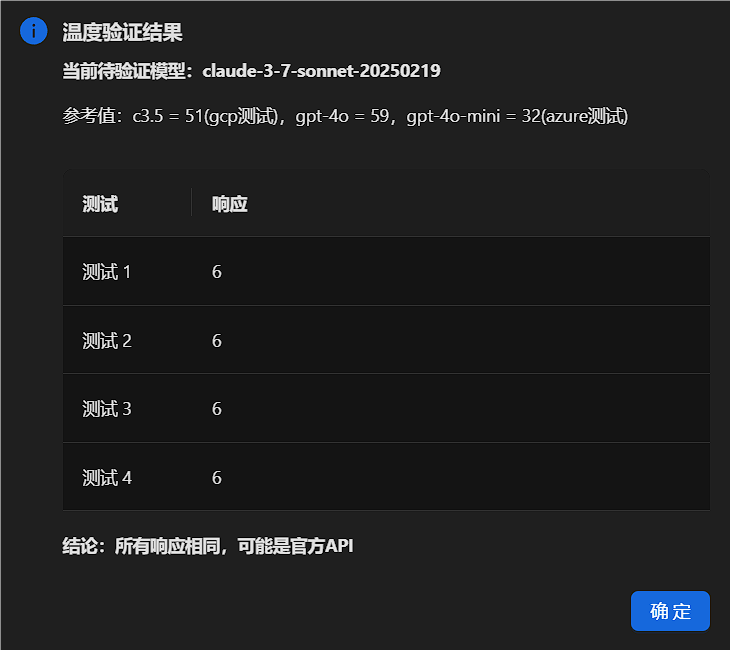
如果数字不是6则为其他低价渠道,可能是逆向或者掺假,来源不明,模型质量无法保证:
某低价中转站:
其他模型官方返回结果参考:
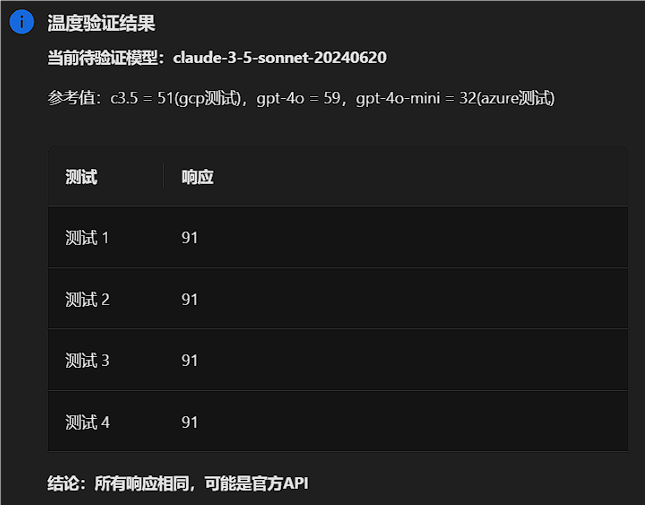
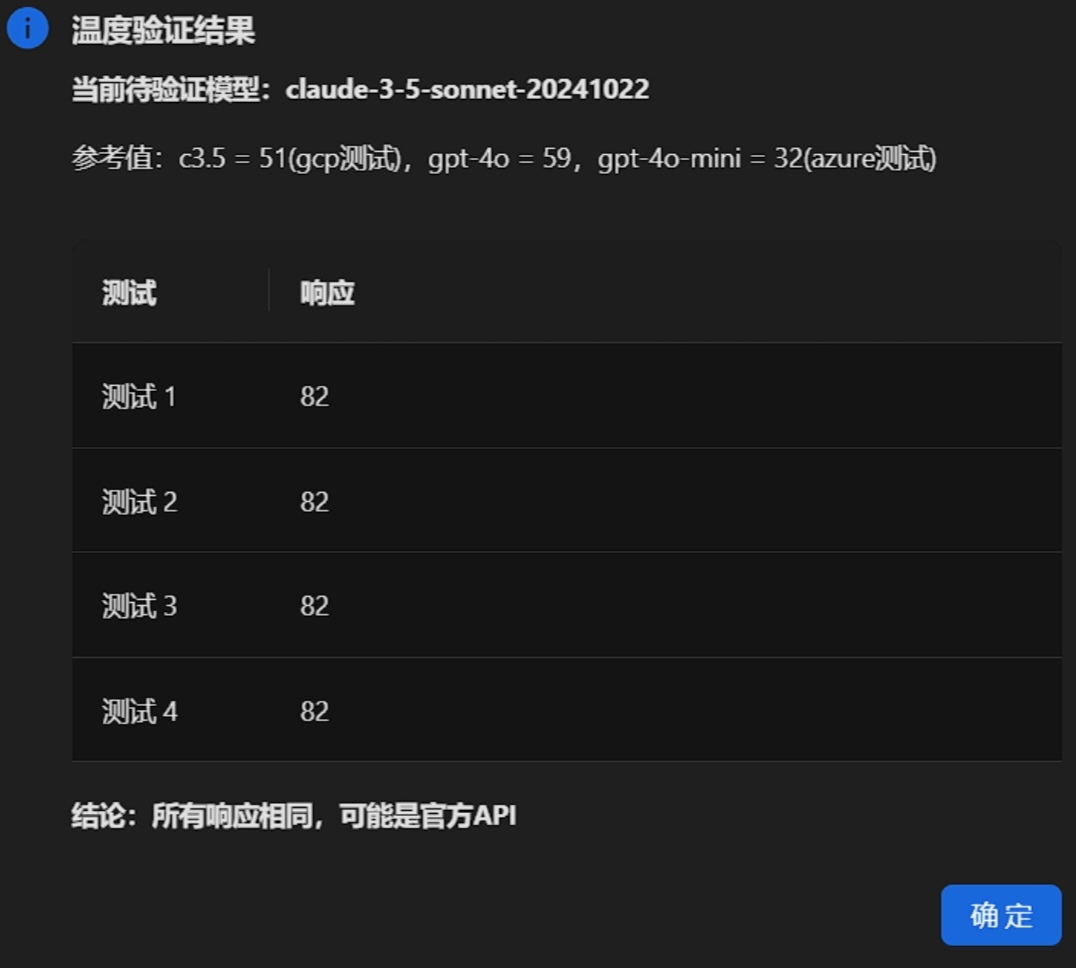
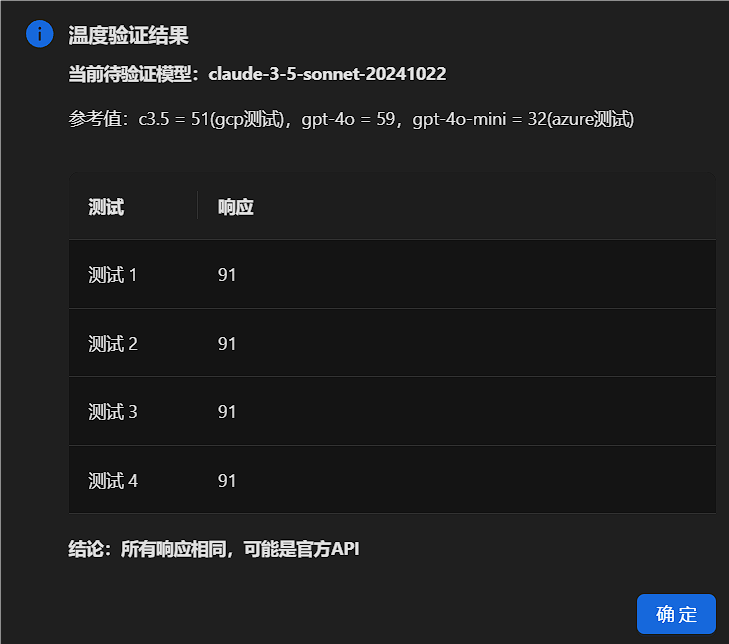
claude-3-5-sonnet-20241022以前是82现在是91
旧站迁移
如果您还是 https://uurzzcoaegnw.gzg.sealos.run 的用户
我们已将旧站 https://uurzzcoaegnw.gzg.sealos.run 中的客户数据迁移至新站 https://api.bailili.top
但是由于数据库的安全验证,旧密码无法直接登录,请移步 https://api.bailili.top
输入您的注册邮箱重置密码登录,重建令牌,方可使用